Πώς να βρείτε το κέντρο ενός κύκλου
Κατά την κατασκευή ή την επεξεργασία εξαρτημάτων ξύλου, σε ορισμένες περιπτώσεις είναι απαραίτητο να προσδιοριστεί πού βρίσκεται το γεωμετρικό τους κέντρο. Εάν το τμήμα έχει τετράγωνο ή ορθογώνιο σχήμα, τότε αυτό δεν είναι δύσκολο να γίνει. Αρκεί να συνδέσουμε απέναντι γωνίες με διαγώνιες, οι οποίες θα τέμνονται ακριβώς στο κέντρο της φιγούρας μας.
Για προϊόντα που έχουν σχήμα κύκλου, αυτή η λύση δεν θα λειτουργήσει, αφού δεν έχουν γωνίες, άρα και διαγώνιες. Σε αυτή την περίπτωση, χρειάζεται κάποια άλλη προσέγγιση, βασισμένη σε διαφορετικές αρχές.

Και υπάρχουν, και σε πολλές παραλλαγές. Μερικά από αυτά είναι αρκετά περίπλοκα και απαιτούν πολλά εργαλεία, άλλα είναι εύκολο να εφαρμοστούν και δεν απαιτούν ένα ολόκληρο σύνολο συσκευών.
Τώρα θα δούμε έναν από τους απλούστερους τρόπους για να βρείτε το κέντρο ενός κύκλου χρησιμοποιώντας μόνο έναν κανονικό χάρακα και μολύβι.
1. Αρχικά, πρέπει να θυμόμαστε ότι η χορδή είναι μια ευθεία γραμμή που συνδέει δύο σημεία σε έναν κύκλο και δεν διέρχεται από το κέντρο του κύκλου.Δεν είναι καθόλου δύσκολο να αναπαραχθεί: απλά πρέπει να τοποθετήσετε έναν χάρακα στον κύκλο οπουδήποτε έτσι ώστε να τέμνει τον κύκλο σε δύο σημεία και να σχεδιάσετε μια ευθεία γραμμή με ένα μολύβι. Το τμήμα μέσα στον κύκλο θα είναι η χορδή.
Κατ 'αρχήν, μπορείτε να τα βγάλετε πέρα με μία χορδή, αλλά για να αυξήσετε την ακρίβεια της δημιουργίας του κέντρου του κύκλου, θα σχεδιάσουμε τουλάχιστον ένα ζευγάρι, ή ακόμα καλύτερα - 3, 4 ή 5 συγχορδίες διαφορετικού μήκους. Αυτό θα μας επιτρέψει να εξομαλύνουμε τα λάθη στις κατασκευές μας και να αντιμετωπίσουμε με μεγαλύτερη ακρίβεια την εργασία.
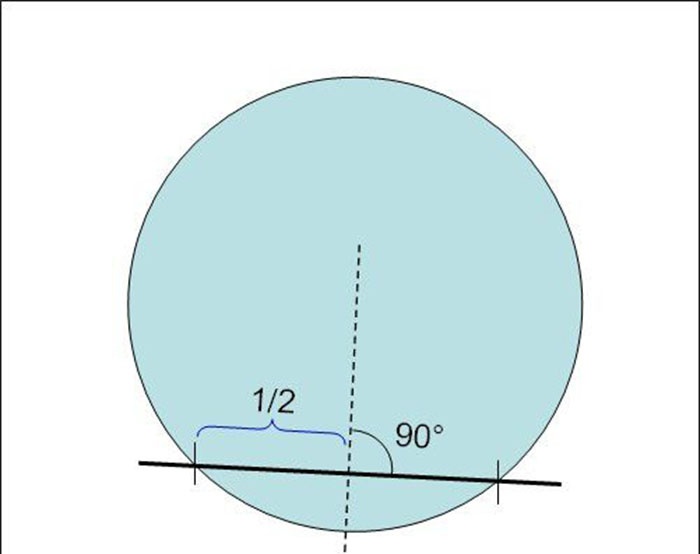
2. Στη συνέχεια, χρησιμοποιώντας τον ίδιο χάρακα, βρίσκουμε τα μεσαία σημεία των συγχορδιών που αναπαράγαμε. Για παράδειγμα, εάν το συνολικό μήκος μιας χορδής είναι 28 cm, τότε το κέντρο της θα βρίσκεται σε ένα σημείο που απέχει 14 cm σε ευθεία γραμμή από την τομή της χορδής με τον κύκλο.
Έχοντας καθορίσει τα κέντρα όλων των χορδών με αυτόν τον τρόπο, σχεδιάζουμε κάθετες γραμμές μέσω αυτών, χρησιμοποιώντας, για παράδειγμα, ένα ορθογώνιο τρίγωνο.
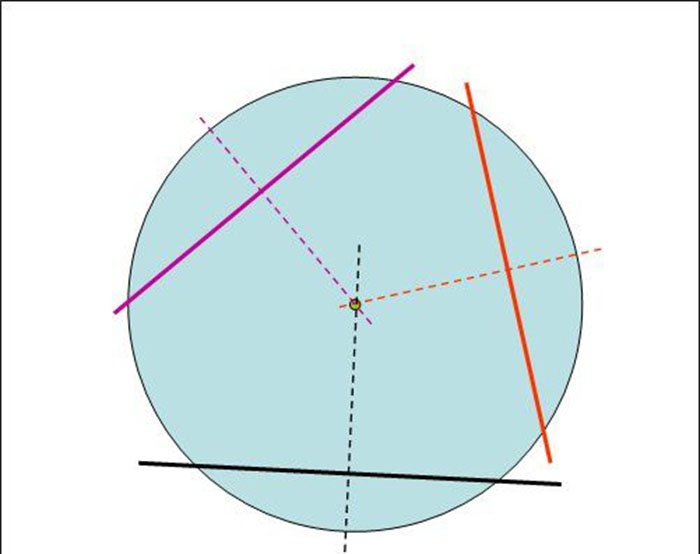

3. Αν τώρα συνεχίσουμε αυτές τις ευθείες κάθετες στις χορδές με κατεύθυνση προς το κέντρο του κύκλου, τότε αυτές θα τέμνονται περίπου σε ένα σημείο, που θα είναι το επιθυμητό κέντρο του κύκλου.

4. Έχοντας καθορίσει τη θέση του κέντρου του συγκεκριμένου κύκλου μας, μπορούμε να χρησιμοποιήσουμε αυτό το γεγονός για διάφορους σκοπούς. Έτσι, αν τοποθετήσετε το πόδι της πυξίδας ενός ξυλουργού σε αυτό το σημείο, μπορείτε να σχεδιάσετε έναν ιδανικό κύκλο και στη συνέχεια να κόψετε έναν κύκλο χρησιμοποιώντας το κατάλληλο εργαλείο κοπής και το κεντρικό σημείο του κύκλου που έχουμε καθορίσει.


Για προϊόντα που έχουν σχήμα κύκλου, αυτή η λύση δεν θα λειτουργήσει, αφού δεν έχουν γωνίες, άρα και διαγώνιες. Σε αυτή την περίπτωση, χρειάζεται κάποια άλλη προσέγγιση, βασισμένη σε διαφορετικές αρχές.

Και υπάρχουν, και σε πολλές παραλλαγές. Μερικά από αυτά είναι αρκετά περίπλοκα και απαιτούν πολλά εργαλεία, άλλα είναι εύκολο να εφαρμοστούν και δεν απαιτούν ένα ολόκληρο σύνολο συσκευών.
Τώρα θα δούμε έναν από τους απλούστερους τρόπους για να βρείτε το κέντρο ενός κύκλου χρησιμοποιώντας μόνο έναν κανονικό χάρακα και μολύβι.
Η ακολουθία εύρεσης του κέντρου του κύκλου:
1. Αρχικά, πρέπει να θυμόμαστε ότι η χορδή είναι μια ευθεία γραμμή που συνδέει δύο σημεία σε έναν κύκλο και δεν διέρχεται από το κέντρο του κύκλου.Δεν είναι καθόλου δύσκολο να αναπαραχθεί: απλά πρέπει να τοποθετήσετε έναν χάρακα στον κύκλο οπουδήποτε έτσι ώστε να τέμνει τον κύκλο σε δύο σημεία και να σχεδιάσετε μια ευθεία γραμμή με ένα μολύβι. Το τμήμα μέσα στον κύκλο θα είναι η χορδή.
Κατ 'αρχήν, μπορείτε να τα βγάλετε πέρα με μία χορδή, αλλά για να αυξήσετε την ακρίβεια της δημιουργίας του κέντρου του κύκλου, θα σχεδιάσουμε τουλάχιστον ένα ζευγάρι, ή ακόμα καλύτερα - 3, 4 ή 5 συγχορδίες διαφορετικού μήκους. Αυτό θα μας επιτρέψει να εξομαλύνουμε τα λάθη στις κατασκευές μας και να αντιμετωπίσουμε με μεγαλύτερη ακρίβεια την εργασία.

2. Στη συνέχεια, χρησιμοποιώντας τον ίδιο χάρακα, βρίσκουμε τα μεσαία σημεία των συγχορδιών που αναπαράγαμε. Για παράδειγμα, εάν το συνολικό μήκος μιας χορδής είναι 28 cm, τότε το κέντρο της θα βρίσκεται σε ένα σημείο που απέχει 14 cm σε ευθεία γραμμή από την τομή της χορδής με τον κύκλο.
Έχοντας καθορίσει τα κέντρα όλων των χορδών με αυτόν τον τρόπο, σχεδιάζουμε κάθετες γραμμές μέσω αυτών, χρησιμοποιώντας, για παράδειγμα, ένα ορθογώνιο τρίγωνο.


3. Αν τώρα συνεχίσουμε αυτές τις ευθείες κάθετες στις χορδές με κατεύθυνση προς το κέντρο του κύκλου, τότε αυτές θα τέμνονται περίπου σε ένα σημείο, που θα είναι το επιθυμητό κέντρο του κύκλου.

4. Έχοντας καθορίσει τη θέση του κέντρου του συγκεκριμένου κύκλου μας, μπορούμε να χρησιμοποιήσουμε αυτό το γεγονός για διάφορους σκοπούς. Έτσι, αν τοποθετήσετε το πόδι της πυξίδας ενός ξυλουργού σε αυτό το σημείο, μπορείτε να σχεδιάσετε έναν ιδανικό κύκλο και στη συνέχεια να κόψετε έναν κύκλο χρησιμοποιώντας το κατάλληλο εργαλείο κοπής και το κεντρικό σημείο του κύκλου που έχουμε καθορίσει.


Παρόμοια master classes
Ιδιαίτερα ενδιαφέρον

Πώς να κρύψετε μια βίδα με αυτοκόλλητη βίδα σε ξύλο

Πώς να επαναφέρετε ένα μαχαίρι εάν σπάσει η λαβή

7 τρόποι για την αξιόπιστη επισκευή των σχισμένων μεντεσέδων από μοριοσανίδες

Πώς να φτιάξετε γερές λαβές λίμας χρησιμοποιώντας πλαστικό

Τρία χρήσιμα κόλπα κατά την εργασία με ξύλο

Ένα απλό κιόσκι σε 1 μέρα
Σχόλια (11)







