Kaip rasti apskritimo centrą
Gaminant ar apdorojant medines dalis, kai kuriais atvejais reikia nustatyti, kur yra jų geometrinis centras. Jei dalis yra kvadrato arba stačiakampio formos, tai padaryti nėra sunku. Pakanka sujungti priešingus kampus su įstrižainėmis, kurios susikirs tiksliai mūsų figūros centre.
Produktams, kurie turi apskritimo formą, šis sprendimas netiks, nes jie neturi kampų, taigi ir įstrižainių. Šiuo atveju reikia kitokio požiūrio, paremto skirtingais principais.

Ir jie egzistuoja, ir daugybe variantų. Kai kurie iš jų yra gana sudėtingi ir reikalauja kelių įrankių, kiti yra lengvai įgyvendinami ir nereikalauja viso įrenginių rinkinio.
Dabar pažvelgsime į vieną iš paprasčiausių būdų, kaip rasti apskritimo centrą naudojant tik įprastą liniuotę ir pieštuką.
1. Pirma, turime atsiminti, kad styga yra tiesi linija, jungianti du apskritimo taškus ir nekertanti apskritimo centro.Atgaminti visai nesunku: tereikia ant apskritimo bet kur padėti liniuotę, kad ji dviejose vietose kirstų apskritimą, ir pieštuku nubrėžti tiesią liniją. Atkarpa apskritimo viduje bus styga.
Iš principo galima apsieiti ir su vienu akordu, bet kad būtų didesnis apskritimo centro nustatymo tikslumas, nubrėžsime bent porą, o dar geriau – 3, 4 ar 5 skirtingo ilgio akordus. Tai leis mums išlyginti mūsų konstrukcijų klaidas ir tiksliau susidoroti su užduotimi.
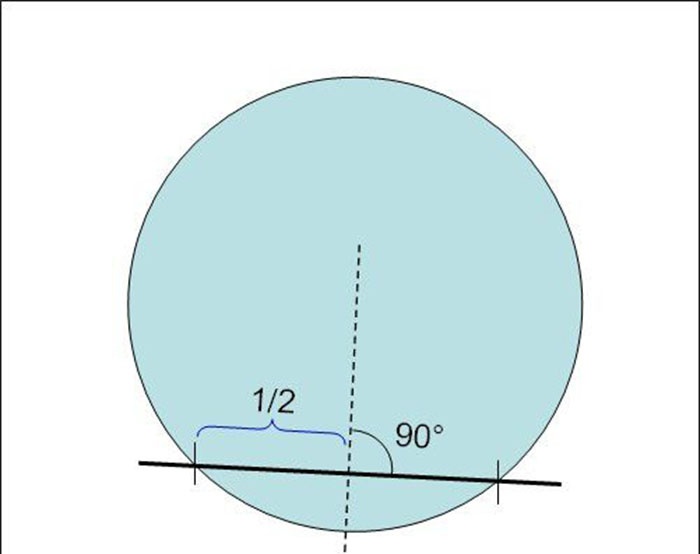
2. Toliau, naudodami tą pačią liniuotę, randame atkurtų stygų vidurio taškus. Pavyzdžiui, jei bendras vienos stygos ilgis yra 28 cm, tai jos centras bus taške, kuris yra 14 cm tiesia linija nuo stygos susikirtimo su apskritimu.
Tokiu būdu nustatę visų stygų centrus, per juos brėžiame statmenas linijas, naudodamiesi, pavyzdžiui, stačiu trikampiu.
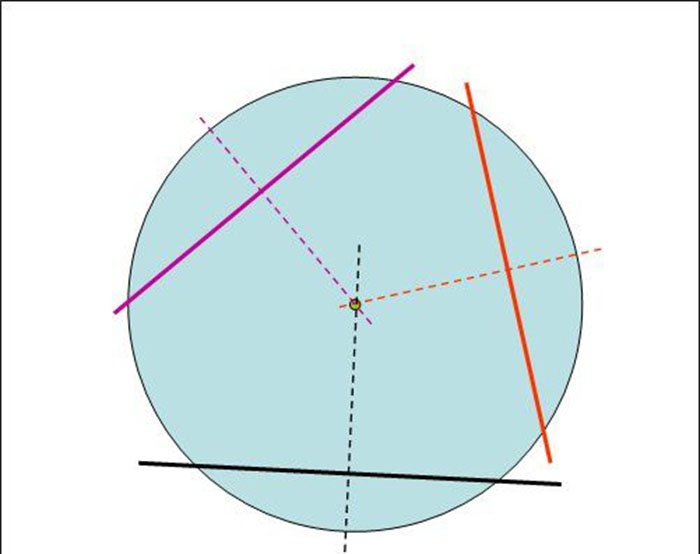

3. Jeigu dabar šias tieses tęsime statmenai stygoms kryptimi į apskritimo centrą, tai jos susikirs maždaug viename taške, kuris bus norimas apskritimo centras.

4. Nustačius savo konkretaus apskritimo centro vietą, šį faktą galime panaudoti įvairiems tikslams. Taigi, jei įdėsite dailidės kompaso koją į šį tašką, galite nubrėžti idealų apskritimą, o tada iškirpti apskritimą naudodami atitinkamą pjovimo įrankį ir mūsų nustatytą apskritimo centrinį tašką.


Produktams, kurie turi apskritimo formą, šis sprendimas netiks, nes jie neturi kampų, taigi ir įstrižainių. Šiuo atveju reikia kitokio požiūrio, paremto skirtingais principais.

Ir jie egzistuoja, ir daugybe variantų. Kai kurie iš jų yra gana sudėtingi ir reikalauja kelių įrankių, kiti yra lengvai įgyvendinami ir nereikalauja viso įrenginių rinkinio.
Dabar pažvelgsime į vieną iš paprasčiausių būdų, kaip rasti apskritimo centrą naudojant tik įprastą liniuotę ir pieštuką.
Apskritimo centro radimo seka:
1. Pirma, turime atsiminti, kad styga yra tiesi linija, jungianti du apskritimo taškus ir nekertanti apskritimo centro.Atgaminti visai nesunku: tereikia ant apskritimo bet kur padėti liniuotę, kad ji dviejose vietose kirstų apskritimą, ir pieštuku nubrėžti tiesią liniją. Atkarpa apskritimo viduje bus styga.
Iš principo galima apsieiti ir su vienu akordu, bet kad būtų didesnis apskritimo centro nustatymo tikslumas, nubrėžsime bent porą, o dar geriau – 3, 4 ar 5 skirtingo ilgio akordus. Tai leis mums išlyginti mūsų konstrukcijų klaidas ir tiksliau susidoroti su užduotimi.

2. Toliau, naudodami tą pačią liniuotę, randame atkurtų stygų vidurio taškus. Pavyzdžiui, jei bendras vienos stygos ilgis yra 28 cm, tai jos centras bus taške, kuris yra 14 cm tiesia linija nuo stygos susikirtimo su apskritimu.
Tokiu būdu nustatę visų stygų centrus, per juos brėžiame statmenas linijas, naudodamiesi, pavyzdžiui, stačiu trikampiu.


3. Jeigu dabar šias tieses tęsime statmenai stygoms kryptimi į apskritimo centrą, tai jos susikirs maždaug viename taške, kuris bus norimas apskritimo centras.

4. Nustačius savo konkretaus apskritimo centro vietą, šį faktą galime panaudoti įvairiems tikslams. Taigi, jei įdėsite dailidės kompaso koją į šį tašką, galite nubrėžti idealų apskritimą, o tada iškirpti apskritimą naudodami atitinkamą pjovimo įrankį ir mūsų nustatytą apskritimo centrinį tašką.


Panašios meistriškumo klasės
Ypatingai įdomu
Komentarai (11)













