Hoe het middelpunt van een cirkel te vinden
Bij het vervaardigen of verwerken van houten onderdelen is het in sommige gevallen noodzakelijk om te bepalen waar hun geometrische middelpunt zich bevindt. Als het onderdeel een vierkante of rechthoekige vorm heeft, is dit niet moeilijk. Het is voldoende om tegenovergestelde hoeken met diagonalen te verbinden, die elkaar precies in het midden van onze figuur zullen snijden.
Voor producten die de vorm van een cirkel hebben, zal deze oplossing niet werken, omdat ze geen hoeken hebben en dus geen diagonalen. In dit geval is een andere aanpak nodig, gebaseerd op andere principes.

En ze bestaan, en in talloze variaties. Sommige zijn behoorlijk complex en vereisen verschillende tools, andere zijn eenvoudig te implementeren en vereisen niet een hele reeks apparaten.
Nu zullen we kijken naar een van de eenvoudigste manieren om het middelpunt van een cirkel te vinden met alleen een gewone liniaal en een potlood.
1. Ten eerste moeten we onthouden dat een akkoord een rechte lijn is die twee punten op een cirkel verbindt en niet door het middelpunt van de cirkel gaat.Het is helemaal niet moeilijk om te reproduceren: je hoeft alleen maar een liniaal ergens op de cirkel te plaatsen zodat deze de cirkel op twee plaatsen snijdt, en een rechte lijn te tekenen met een potlood. Het segment binnen de cirkel zal het akkoord zijn.
In principe kun je met één akkoord rondkomen, maar om de nauwkeurigheid van het vaststellen van het middelpunt van de cirkel te vergroten, zullen we op zijn minst een paar tekenen, of nog beter: 3, 4 of 5 akkoorden van verschillende lengtes. Dit zal ons in staat stellen de fouten in onze constructies te egaliseren en de taak nauwkeuriger aan te pakken.
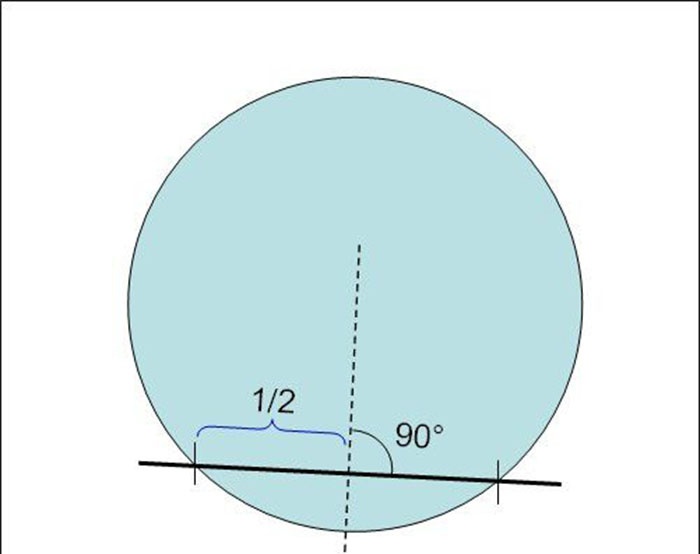
2. Vervolgens vinden we met dezelfde liniaal de middelpunten van de akkoorden die we hebben gereproduceerd. Als de totale lengte van één akkoord bijvoorbeeld 28 cm is, bevindt het middelpunt zich op een punt dat 14 cm in een rechte lijn ligt vanaf het snijpunt van het akkoord met de cirkel.
Nadat we op deze manier de middelpunten van alle akkoorden hebben bepaald, trekken we er loodrechte lijnen doorheen, bijvoorbeeld met een rechthoekige driehoek.
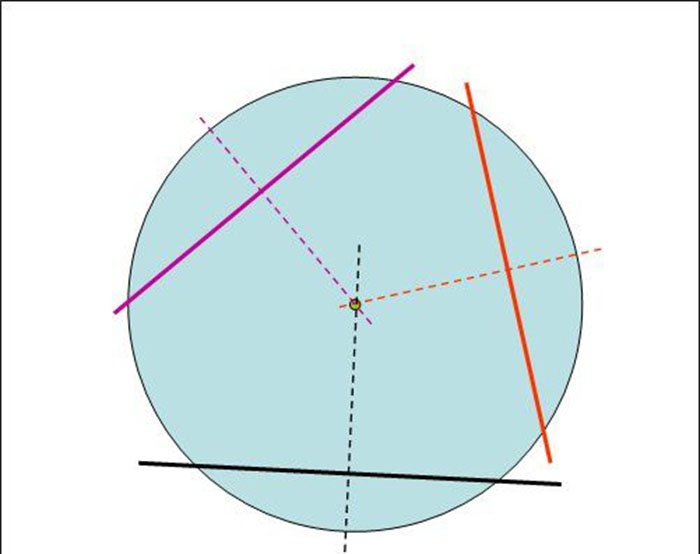

3. Als we nu deze rechte lijnen loodrecht op de koorden voortzetten in de richting naar het middelpunt van de cirkel, dan zullen ze elkaar ongeveer op één punt snijden, wat het gewenste middelpunt van de cirkel zal zijn.

4. Nadat we de locatie van het middelpunt van onze specifieke cirkel hebben vastgesteld, kunnen we dit feit voor verschillende doeleinden gebruiken. Dus als u de poot van een timmermanskompas op dit punt plaatst, kunt u een ideale cirkel tekenen en vervolgens een cirkel uitsnijden met behulp van het juiste snijgereedschap en het middelpunt van de cirkel die we hebben bepaald.


Voor producten die de vorm van een cirkel hebben, zal deze oplossing niet werken, omdat ze geen hoeken hebben en dus geen diagonalen. In dit geval is een andere aanpak nodig, gebaseerd op andere principes.

En ze bestaan, en in talloze variaties. Sommige zijn behoorlijk complex en vereisen verschillende tools, andere zijn eenvoudig te implementeren en vereisen niet een hele reeks apparaten.
Nu zullen we kijken naar een van de eenvoudigste manieren om het middelpunt van een cirkel te vinden met alleen een gewone liniaal en een potlood.
De volgorde van het vinden van het middelpunt van de cirkel:
1. Ten eerste moeten we onthouden dat een akkoord een rechte lijn is die twee punten op een cirkel verbindt en niet door het middelpunt van de cirkel gaat.Het is helemaal niet moeilijk om te reproduceren: je hoeft alleen maar een liniaal ergens op de cirkel te plaatsen zodat deze de cirkel op twee plaatsen snijdt, en een rechte lijn te tekenen met een potlood. Het segment binnen de cirkel zal het akkoord zijn.
In principe kun je met één akkoord rondkomen, maar om de nauwkeurigheid van het vaststellen van het middelpunt van de cirkel te vergroten, zullen we op zijn minst een paar tekenen, of nog beter: 3, 4 of 5 akkoorden van verschillende lengtes. Dit zal ons in staat stellen de fouten in onze constructies te egaliseren en de taak nauwkeuriger aan te pakken.

2. Vervolgens vinden we met dezelfde liniaal de middelpunten van de akkoorden die we hebben gereproduceerd. Als de totale lengte van één akkoord bijvoorbeeld 28 cm is, bevindt het middelpunt zich op een punt dat 14 cm in een rechte lijn ligt vanaf het snijpunt van het akkoord met de cirkel.
Nadat we op deze manier de middelpunten van alle akkoorden hebben bepaald, trekken we er loodrechte lijnen doorheen, bijvoorbeeld met een rechthoekige driehoek.


3. Als we nu deze rechte lijnen loodrecht op de koorden voortzetten in de richting naar het middelpunt van de cirkel, dan zullen ze elkaar ongeveer op één punt snijden, wat het gewenste middelpunt van de cirkel zal zijn.

4. Nadat we de locatie van het middelpunt van onze specifieke cirkel hebben vastgesteld, kunnen we dit feit voor verschillende doeleinden gebruiken. Dus als u de poot van een timmermanskompas op dit punt plaatst, kunt u een ideale cirkel tekenen en vervolgens een cirkel uitsnijden met behulp van het juiste snijgereedschap en het middelpunt van de cirkel die we hebben bepaald.


Soortgelijke masterclasses
Bijzonder interessant
Opmerkingen (11)













