Como encontrar o centro de um círculo
Na fabricação ou processamento de peças de madeira, em alguns casos é necessário determinar onde está localizado seu centro geométrico. Se a peça tiver formato quadrado ou retangular, isso não será difícil de fazer. Basta conectar cantos opostos com diagonais, que se cruzarão exatamente no centro da nossa figura.
Para produtos que possuem formato de círculo, esta solução não funcionará, pois não possuem cantos e, portanto, não possuem diagonais. Neste caso, é necessária alguma outra abordagem, baseada em princípios diferentes.

E eles existem, e em inúmeras variações. Alguns deles são bastante complexos e requerem diversas ferramentas, outros são fáceis de implementar e não requerem um conjunto completo de dispositivos.
Agora veremos uma das maneiras mais simples de encontrar o centro de um círculo usando apenas uma régua e um lápis comuns.
1. Primeiro, precisamos lembrar que uma corda é uma linha reta que conecta dois pontos de um círculo e não passa pelo centro do círculo.Não é nada difícil de reproduzir: basta colocar uma régua no círculo em qualquer lugar para que ela cruze o círculo em dois lugares e desenhar uma linha reta com um lápis. O segmento dentro do círculo será a corda.
Em princípio, você pode conviver com um acorde, mas para aumentar a precisão no estabelecimento do centro do círculo, desenharemos pelo menos alguns, ou melhor ainda - 3, 4 ou 5 acordes de comprimentos diferentes. Isso nos permitirá nivelar os erros em nossas construções e lidar com a tarefa com mais precisão.
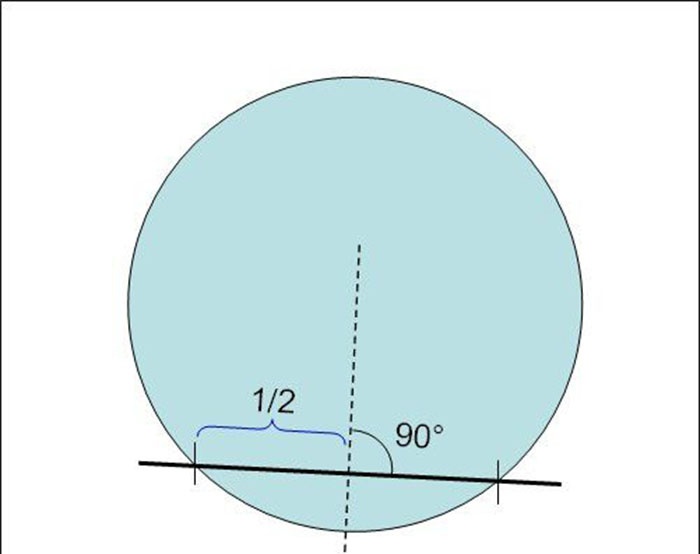
2. A seguir, utilizando a mesma régua, encontramos os pontos médios dos acordes que reproduzimos. Por exemplo, se o comprimento total de uma corda for 28 cm, então seu centro estará em um ponto que fica a 14 cm em linha reta da intersecção da corda com o círculo.
Tendo determinado desta forma os centros de todas as cordas, traçamos linhas perpendiculares através delas, usando, por exemplo, um triângulo retângulo.
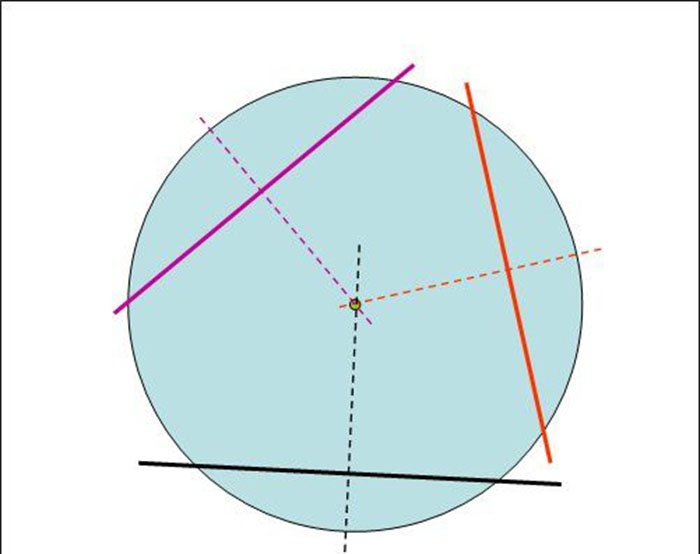

3. Se agora continuarmos essas linhas retas perpendiculares às cordas em direção ao centro do círculo, elas se cruzarão em aproximadamente um ponto, que será o centro desejado do círculo.

4. Tendo estabelecido a localização do centro do nosso círculo específico, podemos usar este facto para vários fins. Portanto, se você colocar a perna de um compasso de carpinteiro neste ponto, poderá desenhar um círculo ideal e, em seguida, recortar um círculo usando a ferramenta de corte apropriada e o ponto central do círculo que determinamos.


Para produtos que possuem formato de círculo, esta solução não funcionará, pois não possuem cantos e, portanto, não possuem diagonais. Neste caso, é necessária alguma outra abordagem, baseada em princípios diferentes.

E eles existem, e em inúmeras variações. Alguns deles são bastante complexos e requerem diversas ferramentas, outros são fáceis de implementar e não requerem um conjunto completo de dispositivos.
Agora veremos uma das maneiras mais simples de encontrar o centro de um círculo usando apenas uma régua e um lápis comuns.
A sequência para encontrar o centro do círculo:
1. Primeiro, precisamos lembrar que uma corda é uma linha reta que conecta dois pontos de um círculo e não passa pelo centro do círculo.Não é nada difícil de reproduzir: basta colocar uma régua no círculo em qualquer lugar para que ela cruze o círculo em dois lugares e desenhar uma linha reta com um lápis. O segmento dentro do círculo será a corda.
Em princípio, você pode conviver com um acorde, mas para aumentar a precisão no estabelecimento do centro do círculo, desenharemos pelo menos alguns, ou melhor ainda - 3, 4 ou 5 acordes de comprimentos diferentes. Isso nos permitirá nivelar os erros em nossas construções e lidar com a tarefa com mais precisão.

2. A seguir, utilizando a mesma régua, encontramos os pontos médios dos acordes que reproduzimos. Por exemplo, se o comprimento total de uma corda for 28 cm, então seu centro estará em um ponto que fica a 14 cm em linha reta da intersecção da corda com o círculo.
Tendo determinado desta forma os centros de todas as cordas, traçamos linhas perpendiculares através delas, usando, por exemplo, um triângulo retângulo.


3. Se agora continuarmos essas linhas retas perpendiculares às cordas em direção ao centro do círculo, elas se cruzarão em aproximadamente um ponto, que será o centro desejado do círculo.

4. Tendo estabelecido a localização do centro do nosso círculo específico, podemos usar este facto para vários fins. Portanto, se você colocar a perna de um compasso de carpinteiro neste ponto, poderá desenhar um círculo ideal e, em seguida, recortar um círculo usando a ferramenta de corte apropriada e o ponto central do círculo que determinamos.


Master classes semelhantes
Particularmente interessante
Comentários (11)













