Како пронаћи центар круга
Приликом производње или обраде дрвених делова, у неким случајевима је потребно утврдити где се налази њихов геометријски центар. Ако део има квадратни или правоугаони облик, онда то није тешко учинити. Довољно је повезати супротне углове дијагоналама, које ће се пресећи тачно у центру наше фигуре.
За производе који имају облик круга, ово решење неће радити, јер немају углове, а самим тим ни дијагонале. У овом случају је потребан неки други приступ, заснован на другачијим принципима.

И постоје, и то у бројним варијацијама. Неки од њих су прилично сложени и захтевају неколико алата, други су лаки за имплементацију и не захтевају читав скуп уређаја.
Сада ћемо погледати један од најједноставнијих начина да пронађете центар круга користећи само обичан лењир и оловку.
1. Прво, треба да запамтимо да је тетива права линија која спаја две тачке на кругу и не пролази кроз центар круга.Уопште није тешко репродуковати: само треба да поставите лењир на круг било где тако да сече круг на два места и нацртајте праву линију оловком. Сегмент унутар круга ће бити тетива.
У принципу, можете проћи са једним акордом, али да бисмо повећали тачност успостављања центра круга, нацртаћемо најмање пар, или још боље - 3, 4 или 5 акорда различитих дужина. Ово ће нам омогућити да изравнамо грешке у нашим конструкцијама и тачније се носимо са задатком.
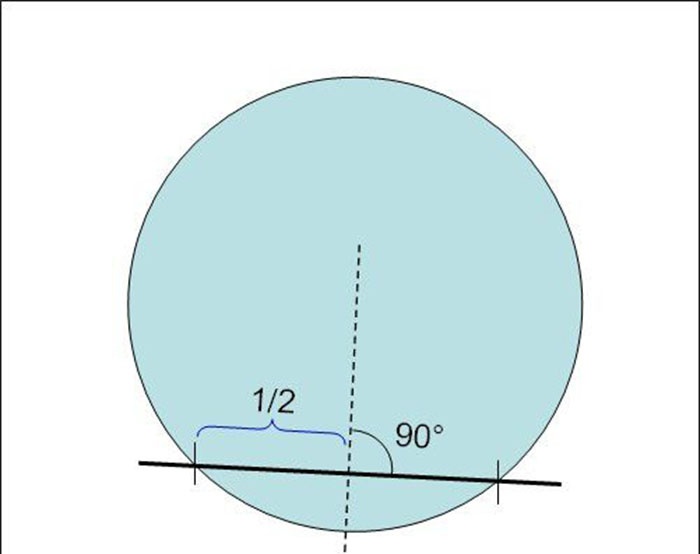
2. Затим, користећи исти лењир, налазимо средине акорда које смо репродуковали. На пример, ако је укупна дужина једне тетиве 28 цм, онда ће њен центар бити у тачки која је 14 цм у правој линији од пресека тетиве са кругом.
Одредивши на овај начин центре свих тетива, кроз њих повлачимо окомите линије, користећи, на пример, правоугли троугао.
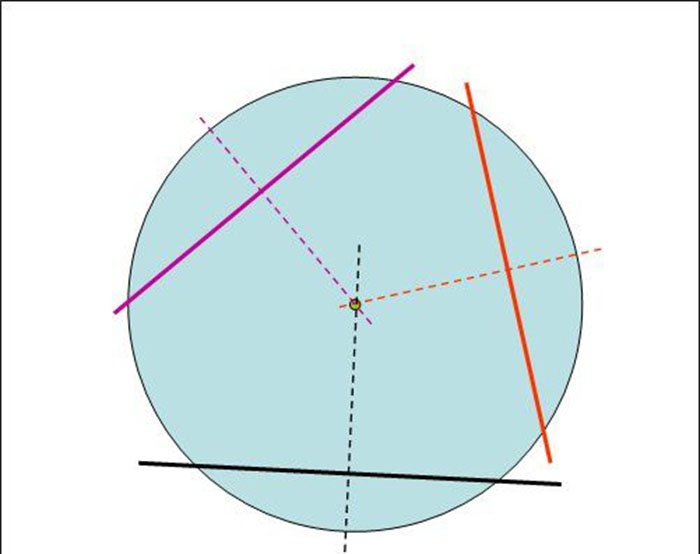

3. Ако сада наставимо ове праве управне на тетиве у правцу центра круга, онда ће се оне пресећи отприлике у једној тачки, која ће бити жељени центар круга.

4. Пошто смо утврдили локацију центра нашег одређеног круга, ову чињеницу можемо искористити у различите сврхе. Дакле, ако поставите ногу столарског шестара на ову тачку, можете нацртати идеалан круг, а затим исећи круг користећи одговарајући алат за сечење и средишњу тачку круга који смо одредили.


За производе који имају облик круга, ово решење неће радити, јер немају углове, а самим тим ни дијагонале. У овом случају је потребан неки други приступ, заснован на другачијим принципима.

И постоје, и то у бројним варијацијама. Неки од њих су прилично сложени и захтевају неколико алата, други су лаки за имплементацију и не захтевају читав скуп уређаја.
Сада ћемо погледати један од најједноставнијих начина да пронађете центар круга користећи само обичан лењир и оловку.
Редослед проналажења центра круга:
1. Прво, треба да запамтимо да је тетива права линија која спаја две тачке на кругу и не пролази кроз центар круга.Уопште није тешко репродуковати: само треба да поставите лењир на круг било где тако да сече круг на два места и нацртајте праву линију оловком. Сегмент унутар круга ће бити тетива.
У принципу, можете проћи са једним акордом, али да бисмо повећали тачност успостављања центра круга, нацртаћемо најмање пар, или још боље - 3, 4 или 5 акорда различитих дужина. Ово ће нам омогућити да изравнамо грешке у нашим конструкцијама и тачније се носимо са задатком.

2. Затим, користећи исти лењир, налазимо средине акорда које смо репродуковали. На пример, ако је укупна дужина једне тетиве 28 цм, онда ће њен центар бити у тачки која је 14 цм у правој линији од пресека тетиве са кругом.
Одредивши на овај начин центре свих тетива, кроз њих повлачимо окомите линије, користећи, на пример, правоугли троугао.


3. Ако сада наставимо ове праве управне на тетиве у правцу центра круга, онда ће се оне пресећи отприлике у једној тачки, која ће бити жељени центар круга.

4. Пошто смо утврдили локацију центра нашег одређеног круга, ову чињеницу можемо искористити у различите сврхе. Дакле, ако поставите ногу столарског шестара на ову тачку, можете нацртати идеалан круг, а затим исећи круг користећи одговарајући алат за сечење и средишњу тачку круга који смо одредили.


Сличне мајсторске класе
Посебно занимљиво
Коментари (11)













