Com trobar el centre d'un cercle
A l'hora de fabricar o processar peces de fusta, en alguns casos cal determinar on es troba el seu centre geomètric. Si la peça té una forma quadrada o rectangular, això no és difícil de fer. N'hi ha prou amb connectar cantonades oposades amb diagonals, que es tallaran exactament al centre de la nostra figura.
Per als productes que tenen forma de cercle, aquesta solució no funcionarà, ja que no tenen cantonades i, per tant, no tenen diagonals. En aquest cas, cal un altre enfocament, basat en principis diferents.

I existeixen, i en nombroses variacions. Alguns d'ells són força complexos i requereixen diverses eines, d'altres són fàcils d'implementar i no requereixen tot un conjunt de dispositius.
Ara veurem una de les maneres més senzilles de trobar el centre d'un cercle utilitzant només un regle normal i un llapis.
1. En primer lloc, hem de recordar que una corda és una recta que uneix dos punts d'una circumferència i que no passa pel centre de la circumferència.No és gens difícil de reproduir: només cal col·locar un regle al cercle a qualsevol lloc perquè talli el cercle en dos llocs i dibuixar una línia recta amb un llapis. El segment dins del cercle serà l'acord.
En principi, us podeu sortir amb un sol acord, però per augmentar la precisió d'establir el centre del cercle, dibuixarem almenys un parell, o encara millor: 3, 4 o 5 acords de diferents longituds. Això ens permetrà anivellar els errors de les nostres construccions i fer front a la tasca amb més precisió.
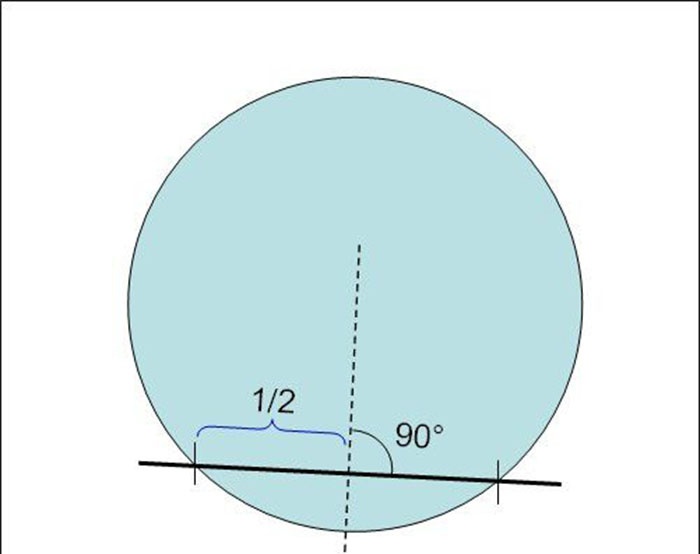
2. A continuació, fent servir el mateix regle, trobem els punts mitjans dels acords que hem reproduït. Per exemple, si la longitud total d'una corda és de 28 cm, llavors el seu centre estarà en un punt que estigui a 14 cm en línia recta des de la intersecció de la corda amb el cercle.
Un cop determinats els centres de totes les cordes d'aquesta manera, tracem línies perpendiculars a través d'elles, utilitzant, per exemple, un triangle rectangle.
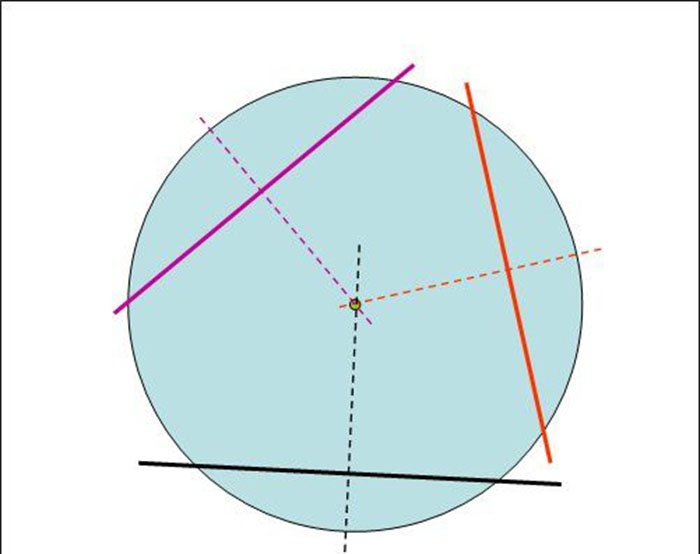

3. Si ara continuem aquestes rectes perpendiculars a les cordes en direcció al centre de la circumferència, llavors es tallaran aproximadament en un punt, que serà el centre desitjat de la circumferència.

4. Un cop establerta la ubicació del centre del nostre cercle particular, podem utilitzar aquest fet per a diversos propòsits. Per tant, si col·loqueu la cama d'una brúixola de fuster en aquest punt, podeu dibuixar un cercle ideal i després retallar-lo amb l'eina de tall adequada i el punt central del cercle que hem determinat.


Per als productes que tenen forma de cercle, aquesta solució no funcionarà, ja que no tenen cantonades i, per tant, no tenen diagonals. En aquest cas, cal un altre enfocament, basat en principis diferents.

I existeixen, i en nombroses variacions. Alguns d'ells són força complexos i requereixen diverses eines, d'altres són fàcils d'implementar i no requereixen tot un conjunt de dispositius.
Ara veurem una de les maneres més senzilles de trobar el centre d'un cercle utilitzant només un regle normal i un llapis.
La seqüència de trobar el centre del cercle:
1. En primer lloc, hem de recordar que una corda és una recta que uneix dos punts d'una circumferència i que no passa pel centre de la circumferència.No és gens difícil de reproduir: només cal col·locar un regle al cercle a qualsevol lloc perquè talli el cercle en dos llocs i dibuixar una línia recta amb un llapis. El segment dins del cercle serà l'acord.
En principi, us podeu sortir amb un sol acord, però per augmentar la precisió d'establir el centre del cercle, dibuixarem almenys un parell, o encara millor: 3, 4 o 5 acords de diferents longituds. Això ens permetrà anivellar els errors de les nostres construccions i fer front a la tasca amb més precisió.

2. A continuació, fent servir el mateix regle, trobem els punts mitjans dels acords que hem reproduït. Per exemple, si la longitud total d'una corda és de 28 cm, llavors el seu centre estarà en un punt que estigui a 14 cm en línia recta des de la intersecció de la corda amb el cercle.
Un cop determinats els centres de totes les cordes d'aquesta manera, tracem línies perpendiculars a través d'elles, utilitzant, per exemple, un triangle rectangle.


3. Si ara continuem aquestes rectes perpendiculars a les cordes en direcció al centre de la circumferència, llavors es tallaran aproximadament en un punt, que serà el centre desitjat de la circumferència.

4. Un cop establerta la ubicació del centre del nostre cercle particular, podem utilitzar aquest fet per a diversos propòsits. Per tant, si col·loqueu la cama d'una brúixola de fuster en aquest punt, podeu dibuixar un cercle ideal i després retallar-lo amb l'eina de tall adequada i el punt central del cercle que hem determinat.


Classes magistrals similars
Particularment interessant
Comentaris (11)













