How to find the center of a circle
When manufacturing or processing wood parts, in some cases it is necessary to determine where their geometric center is located. If the part has a square or rectangular shape, then this is not difficult to do. It is enough to connect opposite corners with diagonals, which will intersect exactly in the center of our figure.
For products that have the shape of a circle, this solution will not work, since they do not have corners, and therefore no diagonals. In this case, some other approach is needed, based on different principles.

And they exist, and in numerous variations. Some of them are quite complex and require several tools, others are easy to implement and do not require a whole set of devices.
Now we will look at one of the simplest ways to find the center of a circle using only a regular ruler and pencil.
1. First, we need to remember that a chord is a straight line connecting two points on a circle and not passing through the center of the circle.It is not at all difficult to reproduce: you just need to place a ruler on the circle anywhere so that it intersects the circle in two places, and draw a straight line with a pencil. The segment inside the circle will be the chord.
In principle, you can get by with one chord, but to increase the accuracy of establishing the center of the circle, we will draw at least a couple, or even better - 3, 4 or 5 chords of different lengths. This will allow us to level out the errors in our constructions and more accurately cope with the task.
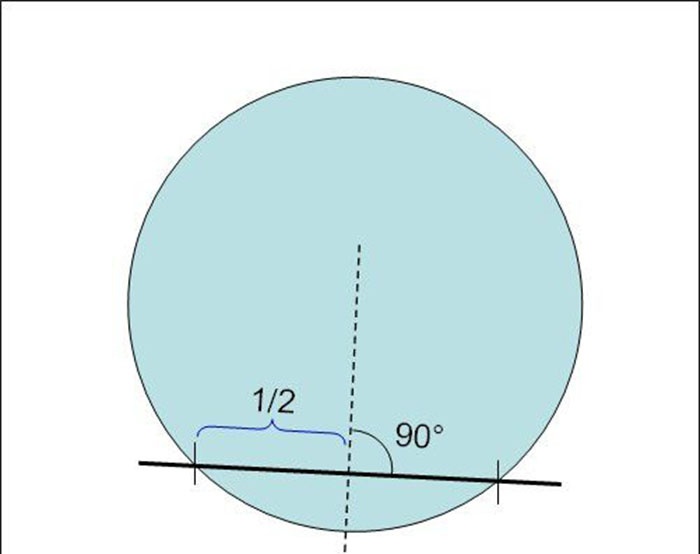
2. Next, using the same ruler, we find the midpoints of the chords we reproduced. For example, if the total length of one chord is 28 cm, then its center will be at a point that is 14 cm in a straight line from the intersection of the chord with the circle.
Having determined the centers of all chords in this way, we draw perpendicular lines through them, using, for example, a right triangle.
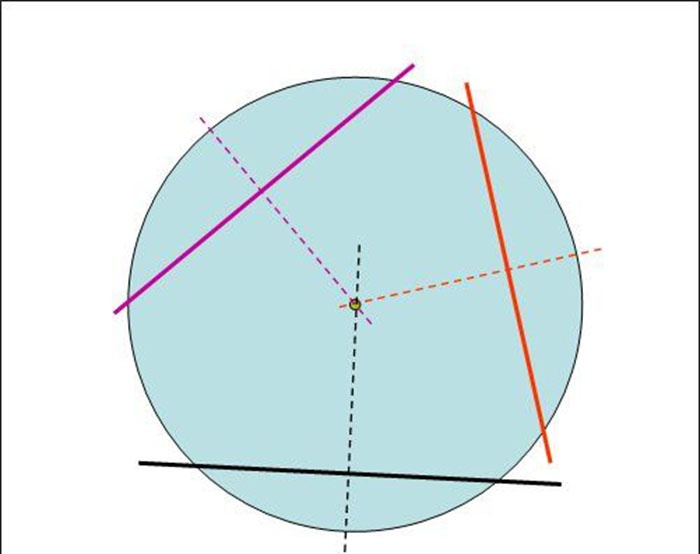

3. If we now continue these straight lines perpendicular to the chords in the direction to the center of the circle, then they will intersect at approximately one point, which will be the desired center of the circle.

4. Having established the location of the center of our particular circle, we can use this fact for various purposes. So, if you place the leg of a carpenter's compass at this point, you can draw an ideal circle, and then cut out a circle using the appropriate cutting tool and the center point of the circle that we have determined.


For products that have the shape of a circle, this solution will not work, since they do not have corners, and therefore no diagonals. In this case, some other approach is needed, based on different principles.

And they exist, and in numerous variations. Some of them are quite complex and require several tools, others are easy to implement and do not require a whole set of devices.
Now we will look at one of the simplest ways to find the center of a circle using only a regular ruler and pencil.
The sequence of finding the center of the circle:
1. First, we need to remember that a chord is a straight line connecting two points on a circle and not passing through the center of the circle.It is not at all difficult to reproduce: you just need to place a ruler on the circle anywhere so that it intersects the circle in two places, and draw a straight line with a pencil. The segment inside the circle will be the chord.
In principle, you can get by with one chord, but to increase the accuracy of establishing the center of the circle, we will draw at least a couple, or even better - 3, 4 or 5 chords of different lengths. This will allow us to level out the errors in our constructions and more accurately cope with the task.

2. Next, using the same ruler, we find the midpoints of the chords we reproduced. For example, if the total length of one chord is 28 cm, then its center will be at a point that is 14 cm in a straight line from the intersection of the chord with the circle.
Having determined the centers of all chords in this way, we draw perpendicular lines through them, using, for example, a right triangle.


3. If we now continue these straight lines perpendicular to the chords in the direction to the center of the circle, then they will intersect at approximately one point, which will be the desired center of the circle.

4. Having established the location of the center of our particular circle, we can use this fact for various purposes. So, if you place the leg of a carpenter's compass at this point, you can draw an ideal circle, and then cut out a circle using the appropriate cutting tool and the center point of the circle that we have determined.


Similar master classes
Particularly interesting
Comments (11)













